Robotics AI Techniques

Course Overview

Robotics AI Techniques focuses on programming self driving cars and autonomous robots. Building a self driving is a huge design and programming challenge. This course focuses on some specific modules that are core to building the self driving cars. The course is inspired and somewhat based on Sebastian Thrun’s books Probabilistic Robotics and Principles of Robot Motion. In fact the course uses Sebastian’s Recorded lectures as the course modules for teaching. We all know that Sebastian Thrun is the “father of self driving cars” and has designed state of the art solutions for the Google Self Driving car and also Stanford Self Driving car. In fact his project of self driving cars led to the foundation of Google Project X which works on finding solutions to the most challenging problems humans face. The course focuses on following major areas of Robotics:

Localization

Localization is the ability for a machine to locate itself in space. The localization program will reduce the margin of error considerably compared to a GPS device, whose margin of error can be as high as ten meters. For our robot to successfully and accurately navigate itself through space, we are looking for a margin of error between two and ten centimeters. The course solves this problem using probabilistic models like Bayes Rule and Total Probability.

Filters

The course explains 3 types of filters, Kalman Filters, Particle Filters and Histogram Filters. All these methods involve significant mathematics to solve the localization problem. The projects are also designed around these methods to localize. The course not only explains the mathematics behind these filters but also walks through the algorithm and the programming behind them.

Planning

The process of finding a path from the start location to the end location is called Robot motion Planning. Basically given a Map, Starting location, Goal Location and cost, we need to find Minimum Cost Path. We get to learn the searching algorithms in AI that are used to locate an object. Specifically we learn the A* algorithm which is one of the most efficient and optimal algorithm in the searching space. In this algorithm we also learn how to use Dynamic Programming to make it efficient.

Control

The course also touches on control algorithm and specifically generating smooth paths. These Smooth paths is what makes the robot follow right turns and avoids it from undershooting and overshooting. This part specifically focuses on PID control and twiddle algorithm to generate values for the P, I and D parameters. A PID controller is a component of a feedback control system. The system (usually called “plant”) is supposed to be maintained at a target “steady” state. For example, a car that needs to stay in the middle of a lane, or a thermostat that needs to maintain a particular temperature, etc.

SLAM

The final module is about Simultaneous Localization and Planning in which the robot is expected to localize and find the path at the same time which is more like the real world scenario. This is based on the Research Paper proposed by Sebastian Thrun himself In this course we particularly focus on Graph SLAM which uses a graph representation to track the landmarks and positions on the robot path.

Lets see some cool Projects of this course

Following are the Projects in this course. Each of the project involves programming the project solution around an interesting problem designed around the above course modules. Each of the project involves significant programming and mathematics. Luckily the projects cover 65% of the grade so grinding on the projects is well worth it.

Kalman Filters - Meteorites

In this project, Earth is threatened by a shower of meteorites falling in your location. It is your task to receive sensor readings of the locations of these meteorites, predict where each of the meteorites will be one tenth of a second later using Kalman Filters (KFs), and finally, destroy each meteorite before it hits the ground by firing your laser turret at it. This project consists of two parts:

1. Estimation: Estimate where meteorites will be one time step into the future (a) Estimation of a small number of meteorites’ positions with no noise in the observations (b) Estimation of the positions of many meteorites given noisy measurements
2. Defense: Aim and fire your laser turret at incoming meteorites before they hit the ground To solve this project, we need to use Kalman Filters with the appropriate tuning of various matrices in it. There are 3 dimensions of Kalman Filters in this project. The position of the meteors, the velocity of the meteors and the acceleration of the meteors. Hence we have 6 parameters to tune in just the F matrix.

My solution involved the following strategies:

1. Define State

• Here the problem uses X and Y as the position. Also the meteorites have some velocity and also acceleration
• Hence state should be with n=6 i.e X=[x, xdot, xdotdot, y, ydot, ydotdot].

2. Based on the state Define F matrix

• Since X is 6D. The F matrix should be 6x6.
• We need to initialize the F matrix based on sigma.

3. Define Uncertainty

• The uncertainty P
• We need to initialize the P matrix based on sigma. Sigma is nothing but difference from the actual value.
• Hence it should be chosen in correspondence with the actual value

Challenges

1. Kalman Filters uses 7 different matrices and we need to specify appropriate value to get an efficient solution. Hence tuning these parameters in the most challenging part
2. Understanding Kalman filters and applying the state model to this problem is also challenging.

Demo

Following is the visualization of my solution where I used Kalman Filters with appropriate tuning to solve the problem. Here each of the particles is the estimated location of the meteorite. The arrow at the bottom is the Laser. As you can see as per the estimates given by Kalman Filter, the laser correctly shoots down the meteors!

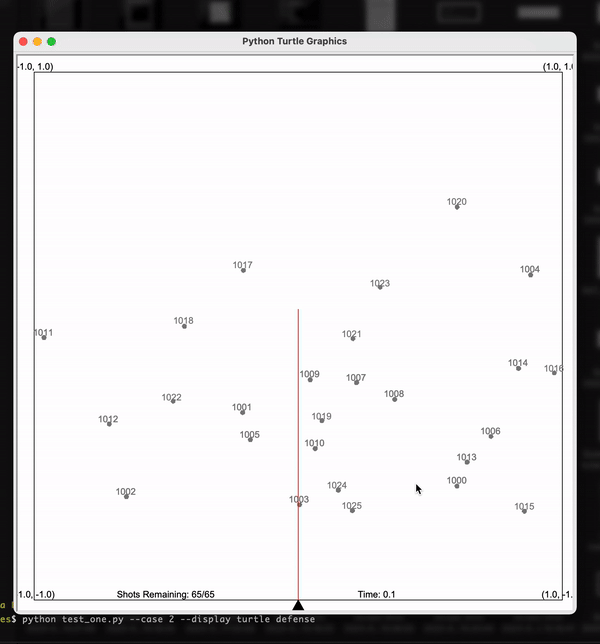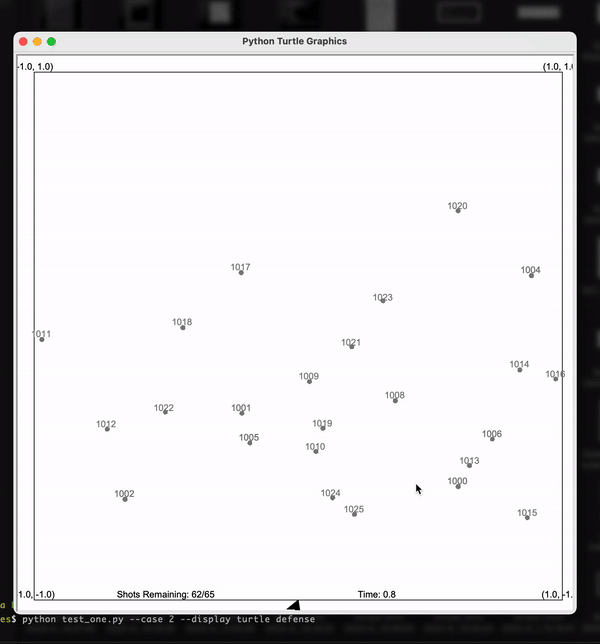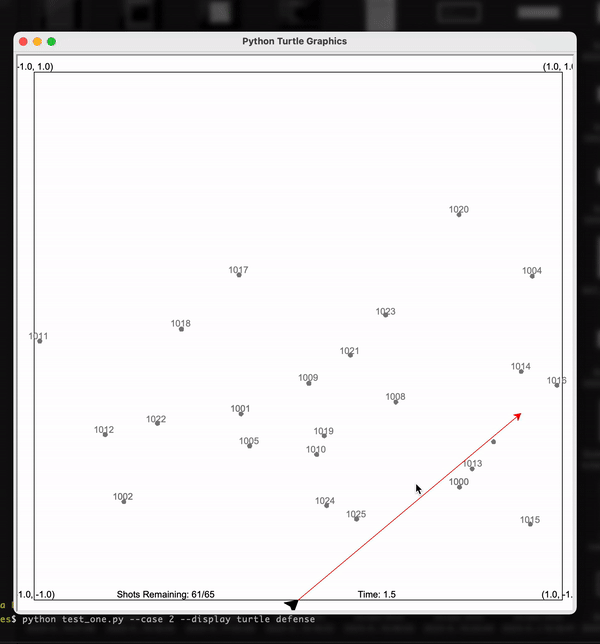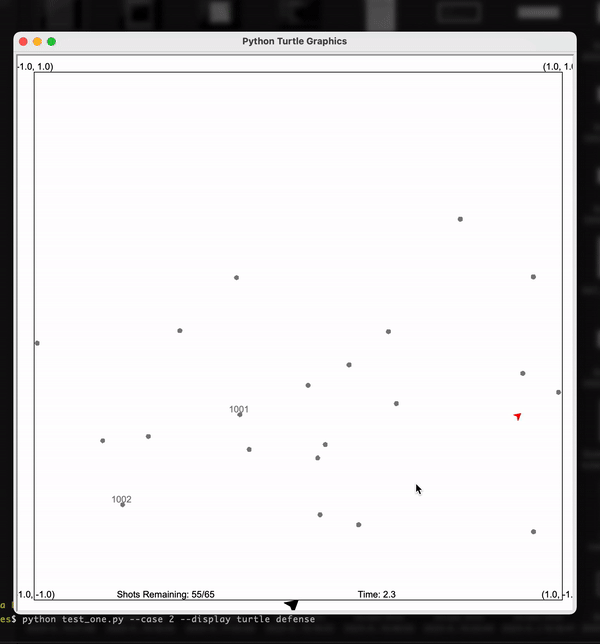
Particle Filters - Solar System

The goal of this project is to practice implementing a particle filter used to localize a man-made satellite in a solar system. After completing an intergalactic mission, it’s time for you to return home. Your satellite is warped through a wormhole and released into your home solar system in perfect circular orbit around the sun. The satellite receives measurements of the magnitude of the collective gravitation pull of the planets in the solar system. Note that this measurement does NOT include the gravitational effects of the sun. Although the gravitational acceleration of other planets can be measured, curiously in your home solar system, the satellite and the planets follow their orbit around the sun and their motion is not affected by other planets. I solved this using Particle filters which uses a Gaussian noise.

Challenges

1. Determining the noise in Gaussian terms was very difficult. You need to really understand what does a Normal Distribution represents.
2. Assigning importance weights is also challenging.
3. Implementing fuzzing is a necessity in the project. You should identify which parameters to fuzz and how much to fuzz their values.

Demo

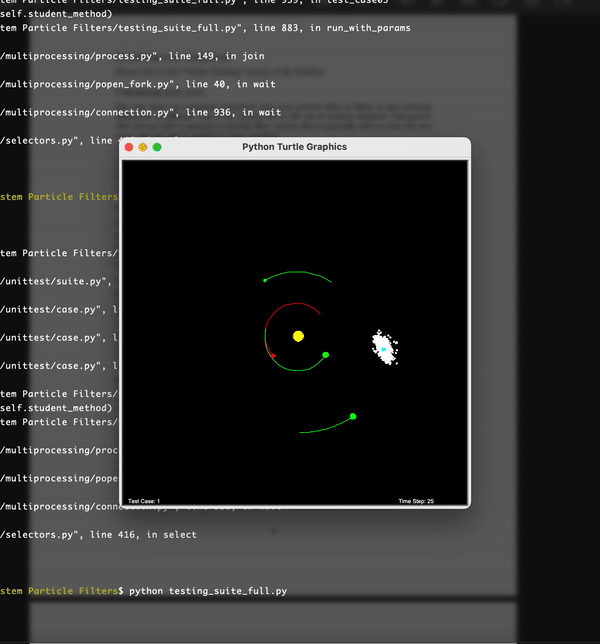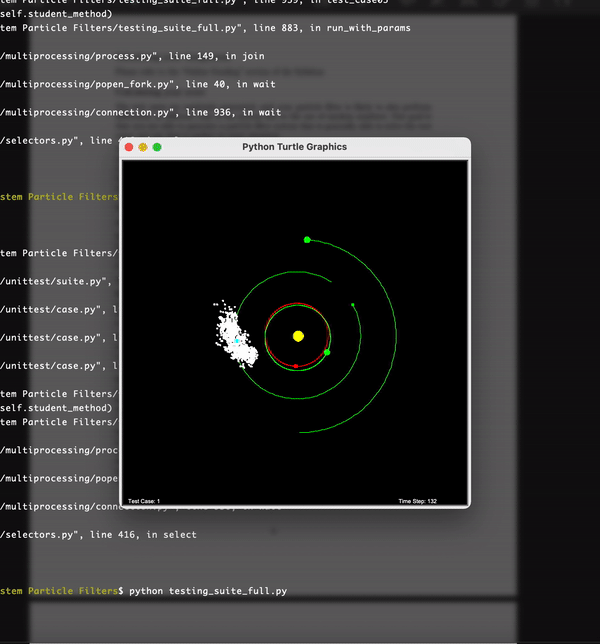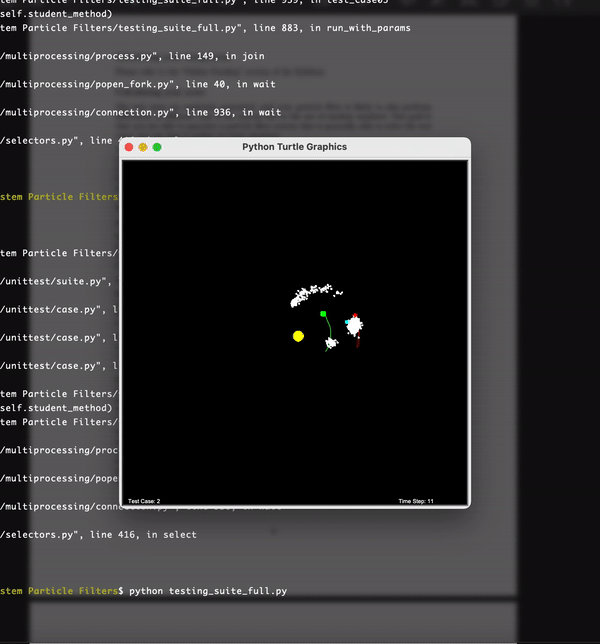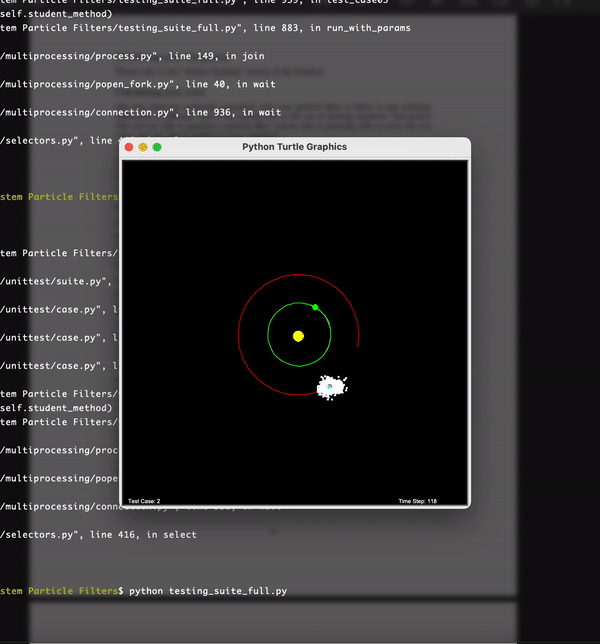
Here each of the white particles is a particle which represents a hypothesis of the estimated location of the satellite. The revolving red body is the satellite and the rest of the bodies are planets. You can see that eventually the particles come closer to the satellite as we estimate the location of the satellite better and better. Hence our hypothesis becomes correct over the time. This is possible by assigning an importance weight to the particles based on the distance between satellite and the particle measurements.

PID Control - Drone Control

This was by far the easiest project and luckily it accounted for the same weight as the other projects. In this project you will be implementing a PID controller to guide a drone to a target elevation and horizontal position and keep it hovering at the target position for a specified time. The Drone starts on the ground with its rotors off. For simplicity we only consider a two dimensional world, and a dual rotor drone. Using the PID controller equations is sufficient to get a decent grade.

Challenges

1. Tuning the values for P, I and D is challenging. You need to understand the relationship between these values and the control of the drone.

Search - Warehouse

This project is very challenging as it involves almost 400-500 lines of coding. In this project, you will implement search algorithms to navigate a robot through a warehouse to pick up and deliver boxes to a designated drop zone area The project is divided into 3 sections:

1. You need to develop A-star algorithm to search for the boxes in the warehouse. Your task is to pick up and deliver all boxes listed in the todo list. You will do this by providing a list of motions that the testing suite will execute in order to complete all the deliveries. Your algorithm should determine the best path to take when completing this task. The A-star algorithm should be optimal and efficient hence we need to use dynamic programming to find the best path.
2. In this part there are three main differences from part A:

• there will be only a single box for your robot to deliver
• the warehouse has an “uneven” floor which imposes an additional cost (range: 0 ~ 95 inclusive)
• the robot starting location is not provided

3. This part becomes even more tricky as the Robot motions are stochastic. Thus we cannot determine surely whether the robot can perform as we want. Hence we need to use probabilities for each of the robot success and failure actions and then determine the best path for the robot.

Challenges

1. Part 3 is the most challenging. I couldn’t complete it fully as I couldn’t understand the calculation of DP memoize step using stochastic probabilities
2. Writing A-star using DP is challenging. You need to pay attention to the lectures thoroughly

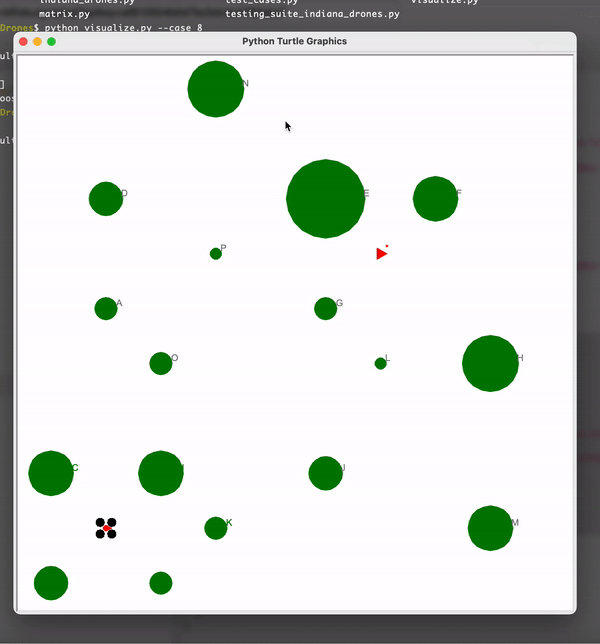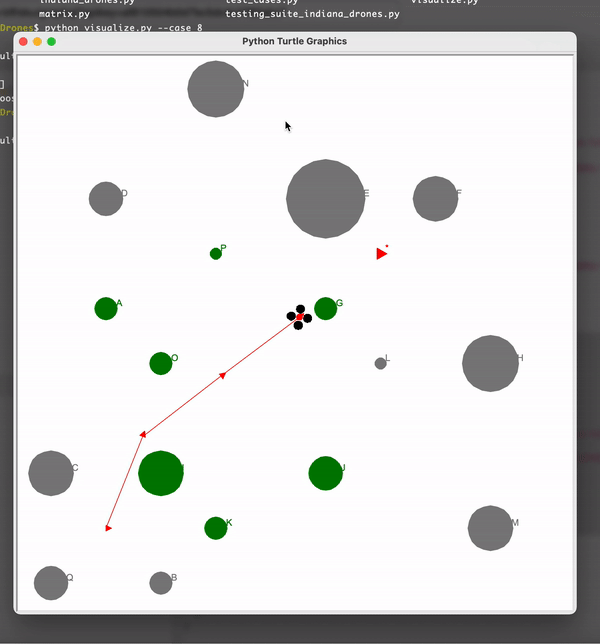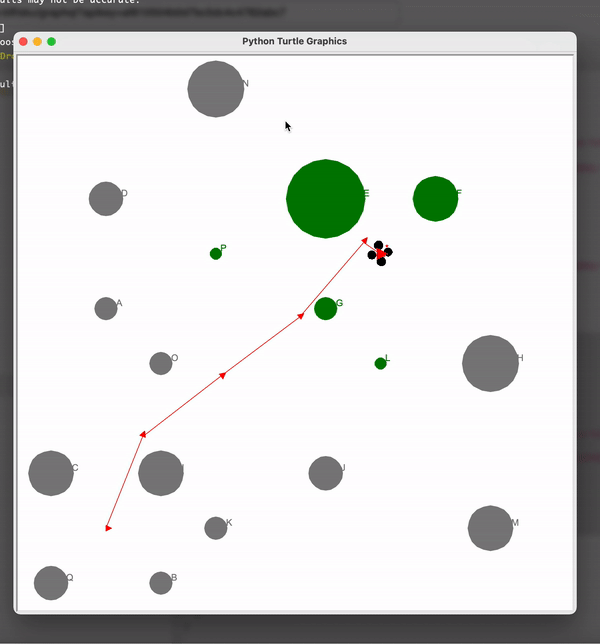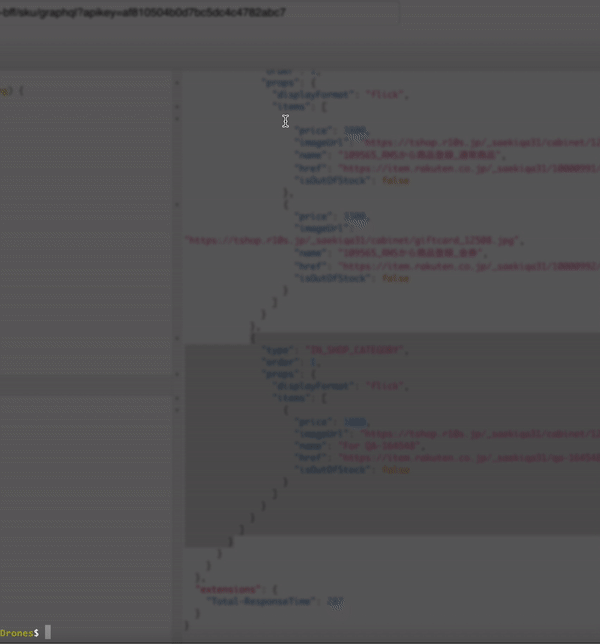
SLAM - Indiana Drones

This was by far the most challenging project in the course. No wonder its the terminal project. Here we need to program a drone to navigate it safely into a jungle surrounded by dense trees. The drones initial position and distances between drone and trees is given. A every time step the drone moves in the jungle. As it moves we need to do the following operations:

1. Estimate the location of the Trees around the drone correctly. Along with that localize the drone so that we are able to estimate the drone location at each time step.
2. Navigate the drone in such a way that the drone avoids collisions into the trees. Also extract the treasure buried at a defined X and Y location. This project is a classic example of the SLAM technique in which we localize and navigate at the same time.

Challenges

1. SLAM theory: Understanding graph-SLAM algorithm and its mathematics is very tricky. You need to model the vanilla algorithm with the problem in the project
2. Navigating the drone was difficult. Avoiding the trees is particularly difficult. Our estimates need to be accurate to avoid the trees.

Demo

In here the black object is the drone’s actual position and the blue trajectory is the estimated path. You can see that the drone closely follows the estimated path. Also the green objects are the trees and the black dot on them is the estimated position of the trees. Hence we have localized the drone as well as the objects along its path.

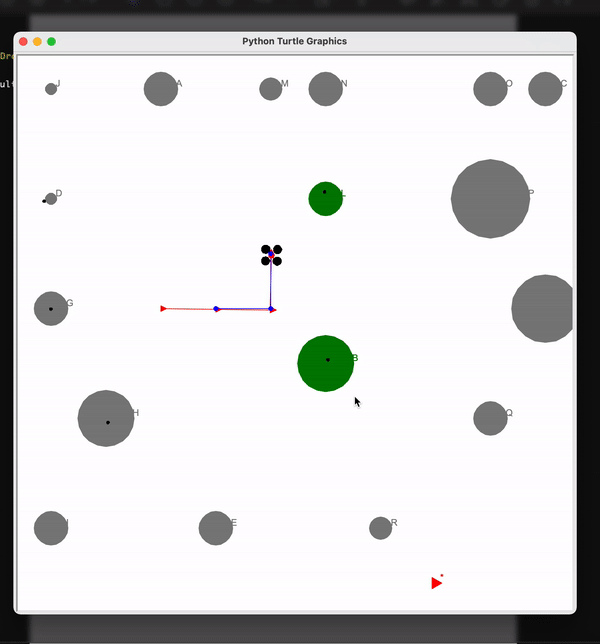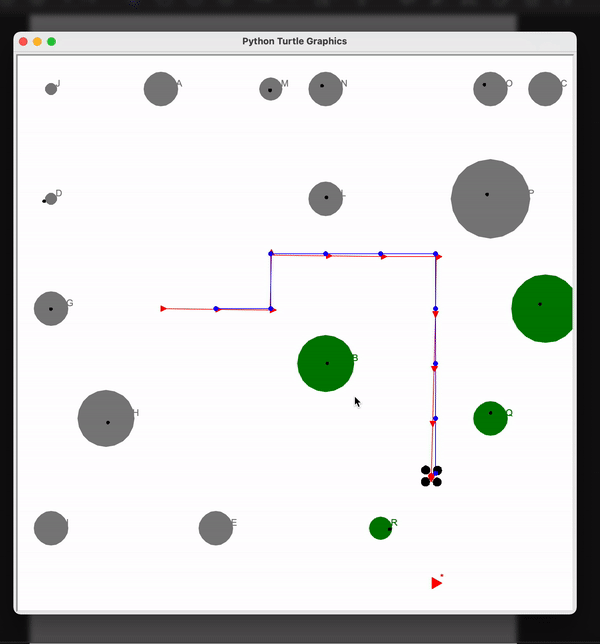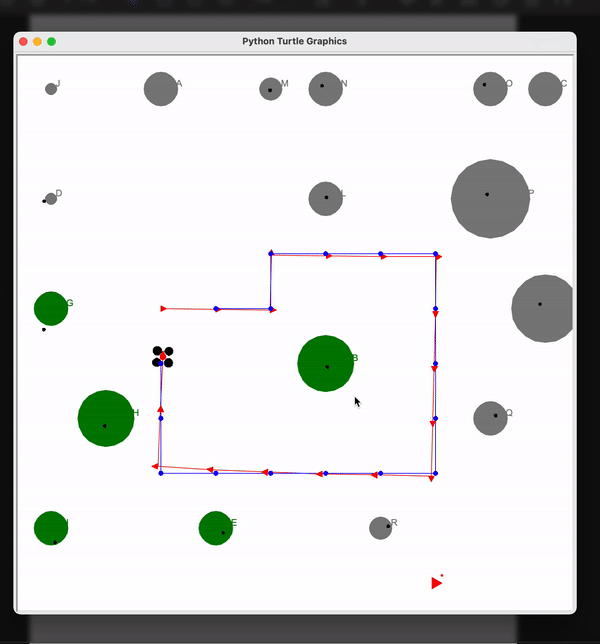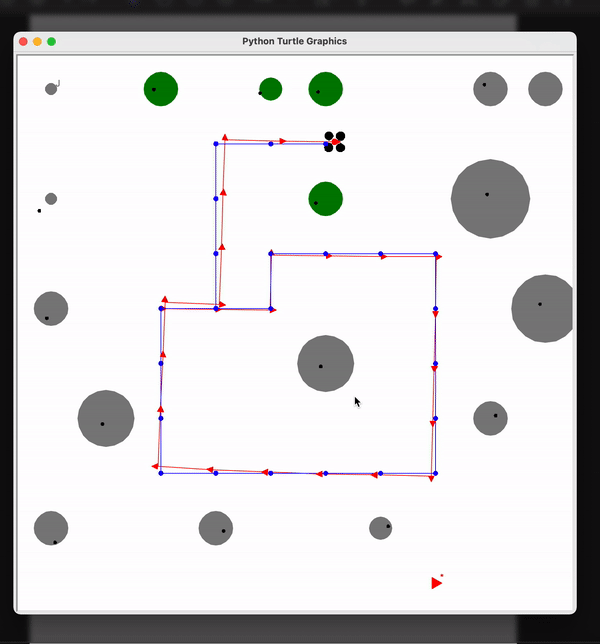
Here you can see that the dron is able to avoid trees in the path and reach the treasure. The obstacles could be avoided because of the predicted positions of drone and the trees